ทฤษฎีกราฟ
ทฤษฎีกราฟ
กราฟมีบทบาทสำคัญกับชีวิตของเราอย่างไร
? ถนนที่เราใช้ในการสัญจรเป็นตัวอย่างหนึ่งที่มีการนำทฤษฎีกราฟมาใช้รวมทั้งการวางระบบท่อประปา
และวงจรไฟฟ้า
ชีวิตประจำวันของเราล้วนเกี่ยวข้องกับคณิตศาสตร์ในเรื่องต่างๆรวมถึงเรื่องทฤษฎีกราฟ
กราฟ G ประกอบด้วยคู่ลำดับของเซต คือ
1.
เซตของจุดยอด (Vertex) ที่ไม่เป็นเซตว่างV(G)
2.
เซตของเส้นเชื่อม(Edge) ระหว่างคู่ที่เชื่อมจุดยอด E(G)
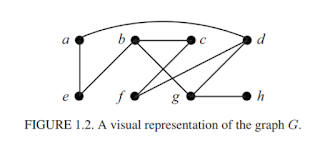
ภาพที่ 1 ภาพประกอบจาก https://www3.nd.edu/~dgalvin1/40210/40210_F12/CGT_early.pdf
จากภาพ เซตของจุดยอด หรือ V(G) คือ { a, b, c, d, e, f, g, h}
เซตของเส้นเชื่อมที่เชื่อมจุดยอด หรือ E(G) คือ {{a, e},{a, d},{b, e},{b, g},{b,
c},{c, f},{d, f},
{d, g}, {g, h}}
จุดยอดประชิด หรือ adjacent vertices คือ
เส้นเชื่อมสองเส้นที่มีจุดยอดเดียวกัน
จากภาพที่ 1 พบว่า
จุดยอด a และ d เป็นจุดยอดประชิด
จุดยอด a และ e เป็นจุดยอดประชิด
จุดยอด b และ e เป็นจุดยอดประชิด
จุดยอด b และ c เป็นจุดยอดประชิด
จุดยอด b และ g เป็นจุดยอดประชิด
จุดยอด c และ f เป็นจุดยอดประชิด
จุดยอด d และ f เป็นจุดยอดประชิด
จุดยอด d และ g เป็นจุดยอดประชิด
จุดยอด g และ h เป็นจุดยอดประชิด
กราฟเชิงเดียว (simple graph) คือ
กราฟที่แต่ละเส้นเชื่อมเชื่อมจุดยอดที่แตกต่างกันและไม่มีเส้นเชื่อมที่ซ้ำกันที่จุดยอดคู่เดียวกัน
ดังภาพต่อไปนี้
ภาพประกอบจาก https://www.researchgate.net/figure/Figure-220-A-graph-and-its-underlying-simple-graph_fig12_317901287
จากภาพเราจะพบว่าภาพแรกหรือภาพทางซ้ายไม่ใช่กราฟเชิงเดียว
(simple graph) เนื่องจากจุด V1 และ
V3 มีเส้นเชื่อมที่ซ้ำกัน นอกจากนี้จุด V2 ยังมีเชื่อมกันที่จุดยอดเดิม หรือที่เราเรียกว่าลูป (loop)
ภาพที่สองหรือภาพทางขวาเป็นกราฟเชิงเดียวหรือ (simple graph) เนื่องจากไม่มีลูปและไม่มีเส้นเชื่อมที่ซ้ำกันที่จุดยอดคู่เดียวกัน
มัลติกราฟ (Multi Graph) คือ
กราฟที่มีเส้นเชื่อมซ้ำกันที่จุดยอดคู่เดียวกันและไม่มีลูป
ภาพประกอบจาก https://www.chegg.com/homework-help/questions-and-answers/1-graph-simple-graph-multigraph-pseudogr
จากภาพ กราฟ G1 เป็นมัลติกราฟ (multi graph) เนื่องจากมีเส้นเชื่อมซ้ำกันที่คู่ของจุดยอด
b,d และคู่ของจุดยอด a,b แต่กราฟ G2 ไม่เป็นมัลติกราฟ เพราะว่ามีลูป แต่จะเป็นมัลติกราฟระบุทิศทางซึ่งจะอธิบายภายหลัง



ความคิดเห็น
แสดงความคิดเห็น